数值孔径(Numerical Aperture, N.A)详解:光学系统的核心参数
一、定义与计算公式
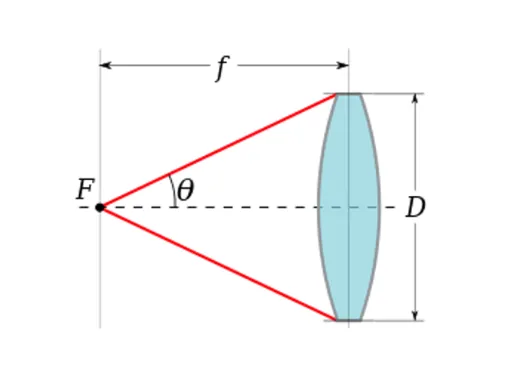
数值孔径(Numerical Aperture, N.A)是衡量光学系统(如显微镜物镜、工业镜头等)收光能力和空间分辨率的关键参数。其定义为:
\( \text{N.A} = n \times \sin(\theta/2) \)
其中:
\( n \):物体与镜头间介质的折射率(如空气\( n=1 \),水\( n=1.33 \),油\( n=1.515 \))
\( \theta \):孔径角(镜口角),即镜头光轴上物体点与前透镜有效直径形成的角度。
孔径角越大,进入透镜的光通量越高,且与透镜有效直径成正比,与焦点距离成反比。
二、数值孔径的影响因素
- 介质折射率(n):增大介质折射率(如使用油浸物镜)可显著提升N.A值。例如:空气介质N.A≤0.95;油浸介质N.A可达1.4以上,溴萘介质甚至可达1.663。
- 孔径角(θ):实际应用中物镜的孔径角通常固定,需通过介质优化提升N.A。
三、数值孔径与其他参数的关系
| 参数 | 关系说明 | 公式或示例 |
|---|---|---|
| 分辨率 | 与N.A成正比,N.A越大能分辨的细节越精细 | \( d=0.61\lambda/\text{N.A} \) |
| 放大率 | 与N.A间接相关,但需注意无效放大(分辨率不足时过度放大导致模糊) | 有效放大率范围≈500~1000×N.A |
| 焦深 | 与N.A²成反比,高N.A系统需更精确调焦 | 焦深≈\( \lambda/(2 \times \text{N.A}^2) \) |
| 视场与工作距离 | N.A增大时,视场范围和工作距离(物镜前透镜到样品的距离)减小 | — |
四、实际应用与选型建议
分辨率优化
短波长光源(如蓝光)结合高N.A物镜可提升分辨率。
物镜选择
高N.A物镜适合细节观测(如细胞结构),低N.A物镜适合大视野场景(如组织切片观察)。需平衡N.A与工作距离:生物活体样本建议选用长工作距离物镜。
介质匹配
油浸物镜需使用专用浸油,避免气泡影响成像。
五、常见误区
误区:“N.A越大越好”
纠正:高N.A可能牺牲景深和工作距离,需根据实验需求(如荧光成像、三维观测)综合选择。
误区:“放大率越高图像越清晰”
纠正:分辨率由N.A决定,超出有效放大率范围会导致图像模糊。
